Push and Pull Search（PPS）[1]是一个非常具有潜力的约束多目标问题求解框架。其中的Push和Pull搜索过程都可以进行自由定制，从而衍生出一系列的约束多目标进化算法。近期，我们提出一种PPS与multi-objective to multi-objective （M2M）分解方法相结合的约束多目标进化算法（PPS-M2M）。该算法将约束多目标优化问题（CMOP）分解为一组简单的CMOP。每个简单的CMOP对应一个子种群，并以协同的方式求解。在处理约束时，每个子种群采用PPS搜索机制，有助于每个子种群跨越不可行的区域，如图1所示。

图1. PPS-M2M搜索行为。将目标空间分为5个子区域（M1 ,M2 ,…, M5）。(a)-(c)展示Push搜索过程，每个子区域的工作子种群在不考虑任何约束的情况下跨越不可行的区域。(d)-(f)展示Pull搜索过程，其中每个子区域中的不可行个体被拉回可行和非支配区域。

       为了测试PPS-M2M的性能，在LIR-CMOPs测试问题上，PPS-M2M算法和9种约束多目标算法（CM2M、 MOEA/D-Epsilon、 MOEA/D-SR、 MOEA/D-CDP、 C-MOEA/D、NSGA-II-CDP、 MODE-ECHM、 CM2M2 和 MODE-SaE）进行比较。图2和图3分别展示了在LIR-CMOP7和LIR-CMOP11上，PPS-M2M和其他9种算法获得的Pareto前沿。

       此外，为了说明PPS-M2M和PPS-MOEA/D之间的差异，我们在MOPs和DAS-CMOPs[2]的基础上设计了一组带约束不平衡多目标优化问题（CIMOPs）。CIMOPs的目标函数与MOPs的目标函数相同，且具有不平衡的特点。CIMOPs的约束函数具有多样性难度特点。图4和图5分别展示了在CIMOP2和CIMOP4上，PPS-M2M和其他三种算法（PPS-MOEA/D、CM2M、CM2M2）获得的Pareto前沿。

图2. 十种算法在LIR-CMOP7上获得Pareto前沿。

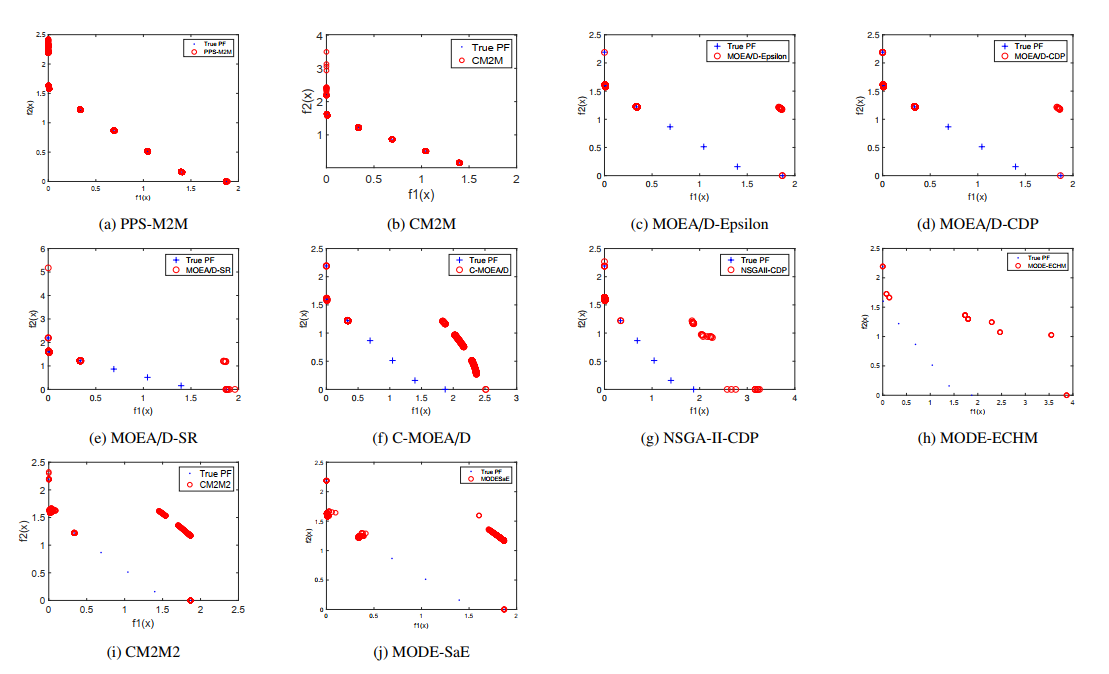
图3. 十种算法在LIR-CMOP11上获得Pareto前沿。

图4. 四种算法在CIMOP2上获得Pareto前沿。

图5. 四种算法在CIMOP4上获得Pareto前沿。

       通过以上实验比较，我们可以总结出PPS-M2M不仅可以解决具有较大不可行区域的CMOPs，还能有效地解决目标函数不平衡和约束函数多样性难度的CMOPs。

[1]     Fan Z, Li W, Cai X, et al. Push and pull search for solving constrained multi-objective optimization problems[J]. Swarm and evolutionary computation, 2019, 44: 665-679.

[2]     Fan Z, Li W, Cai X, et al. Difficulty adjustable and scalable constrained multi-objective test problem toolkit[J]. Evolutionary Computation, 2019: 1-28.

研究成果：发表在人工智能一区期刊《Swarm and Evolutionary Computation 》

论文下载：Download  PDF

源码下载：CODE

论文引用：Fan Z, Wang Z, Li W, et al. Push and pull search embedded in an M2M framework for solving constrained multi-objective optimization problems[J]. Swarm and Evolutionary Computation, 2020: 100651.