最近,范衠教授指导的博士研究生李文姬与南京航空航天大学蔡昕烨教授、西安交通大学李辉教授(MOEA/D发明人之一)、汕头大学韦才敏教授、香港城市大学张青富(Qingfu Zhang)教授(进化计算领域顶级学者,IEEE Fellow)、密歇根州立大学Kalyanmoy Deb教授(进化计算领域顶级学者,IEEE Fellow)和美国BEACON国家科技中心主任Erik Goodman教授共同完成的研究论文《Difficulty Adjustable and Scalable Constrained Multi-objective Test Problem Toolkit》被进化计算领域知名期刊、SCI(计算机科学——理论与方法学科)1区期刊《Evolutionary Computation》录用。另外,SCI(人工智能)1区期刊《Swarm and Evolutionary Computation》于此前收录了他们共同完成的另外一篇研究论文《Push and Pull Search for Solving Constrained Multi-objective Optimization Problems》。两篇论文的第一作者和第二篇论文的通讯作者是汕头大学范衠教授,第一篇论文的通讯作者是南京航空航天大学蔡昕烨教授,两篇论文的第一完成单位均是汕头大学。
在现实世界中,受限于资源、环境等因素的约束,实际工程优化中的问题不可避免的是一个带约束条件的多目标(节能、环保、经济等目标)优化问题。目前在学术界,在约束多目标优化方面的研究工作不仅由于其难度大而相对较少,甚至缺乏能够有效测试约束多目标进化算法性能的测试问题集。上述两篇研究论文分别是在带约束条件的多目标优化测试问题集和进化算法方面取得的重要成果。另外,值得注意的是,在最近美国的商业管制清单中,在人工智能方面,明确把进化和遗传计算(例如遗传算法和遗传编程)列为仅次于神级网络和深度学习的管制技术,这从另一个侧面也说明了上面两篇研究论文的重要意义。
在《Difficulty Adjustable and Scalable Constrained Multi-objective Test Problem Toolkit》一文中,针对现有约束多目标测试问题的不足,定义了一类难度可控,目标和约束数量可调的约束多目标测试问题。首次对约束问题的难度类型进行了定义,提出了三种难度的约束类型,即多样性困难、可行性困难和收敛性困难。三种难度类型的约束能够任意组合,构成同时具有多种难度类型的约束多目标测试问题。每种约束类型的难度都可以自由调整,问题可以进行自由定制,能够全面综合评估约束多目标进化算法在单一难度或多种难度下的性能。论文一经录用,就引起了广泛的关注,甚至在ArXiv上发表时,就得到了大量的引用。
1. 多样性困难的约束:
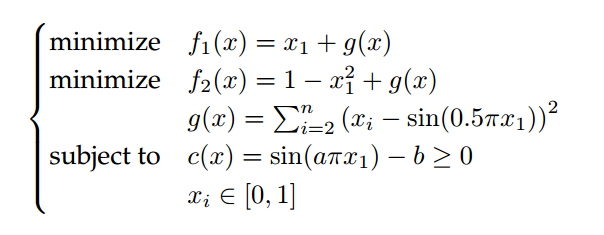
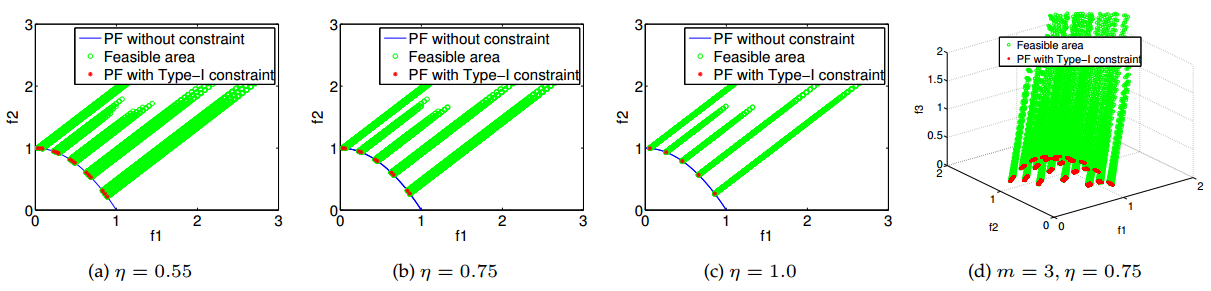
图1 多样性困难的约束函数
2. 可行性困难的约束:
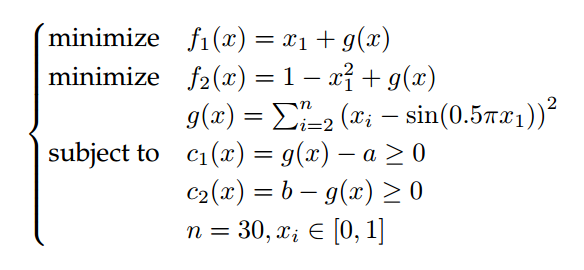
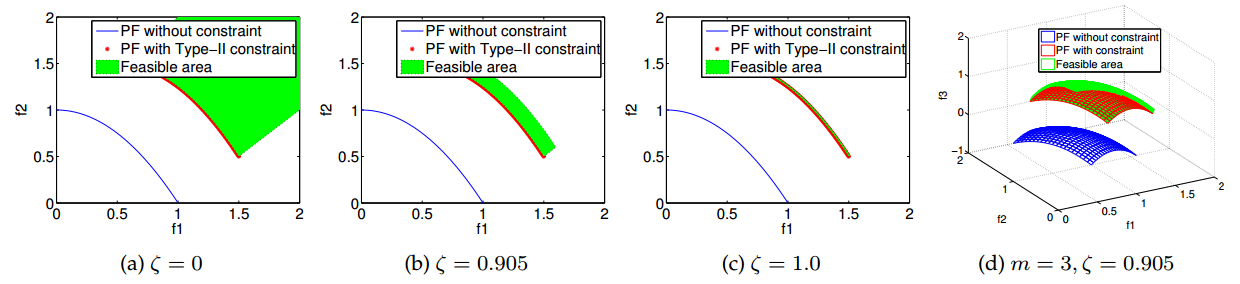
图2 可行性困难的约束函数
3. 收敛性困难的约束:
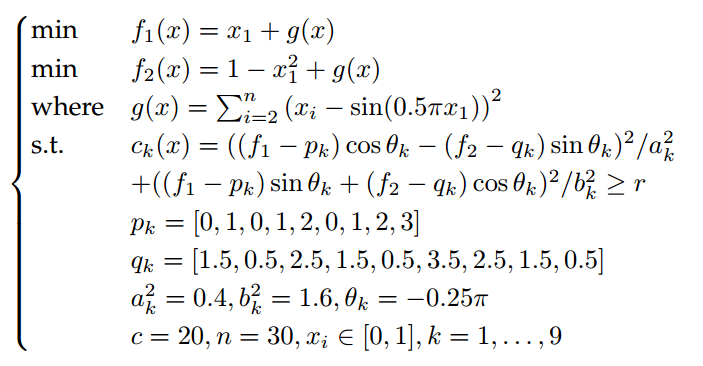
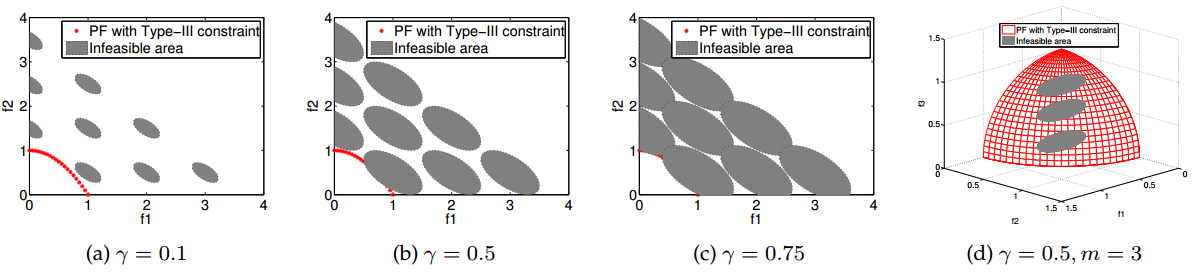
图3 收敛性困难的约束函数
三种难度类型的约束类似于颜色中的三原色,它们之间能够任意组合,生成7种基本难度类型的约束(如图4(a)和表1所示)。每种约束类型的难度大小都可以自由调整,可构造各种难度等级的约束多目标测试问题(如图4(b)所示)。
图4 难度类型和难度等级示意图

此外,所提出的难度可调、目标和约束可扩展的约束多目标测试问题构建框架(如下图所示)还可以构造约束高维目标(目标个数大于等于4)优化问题。
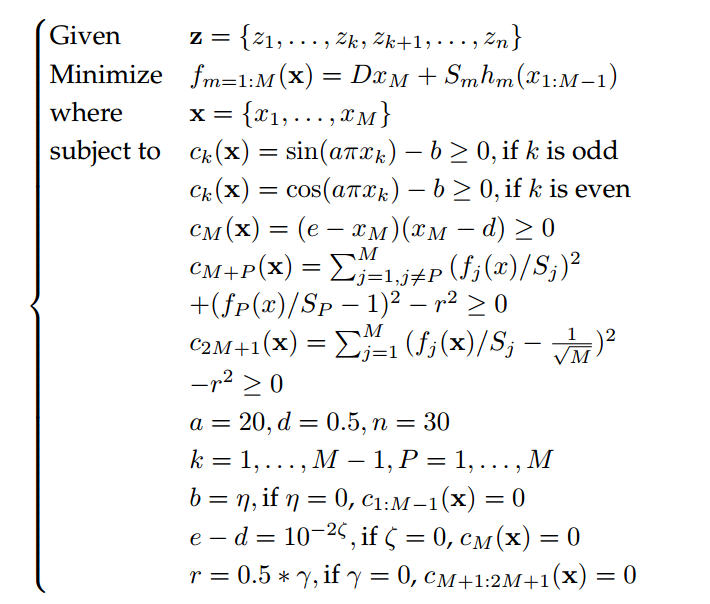
图5 难度可调、目标和约束可扩展的约束多目标测试问题构建框架
在《Push and Pull Search for Solving Constrained Multi-objective Optimization Problems》一文中,提出了一种Push和Pull的搜索框架(PPS)(见图6),其采用从无约束Pareto前沿反向搜索约束Pareto前沿的思想,从而有效克服了传统约束多目标进化算法无法跨越多个不可行区的难题(见图7)。PPS算法把整个搜索过程分为Push 和 Pull两个阶段。在Push阶段,采用多目标进化算法(MOEA)在不考虑约束的情况下探索整个搜索区域,从而有助于快速的跨越不可行区域,得到无约束的Pareto前沿。此外,约束违反程度的信息也能够被探测和估计。在Pull阶段,采用改进的epsilon约束处理机制并利用探测到的约束违反信息,把整个种群拉回到可行的非支配区域。所提出的PPS算法在IGD指标方面比其他当前最好的6种算法提升1-2个数量级(见图8)。
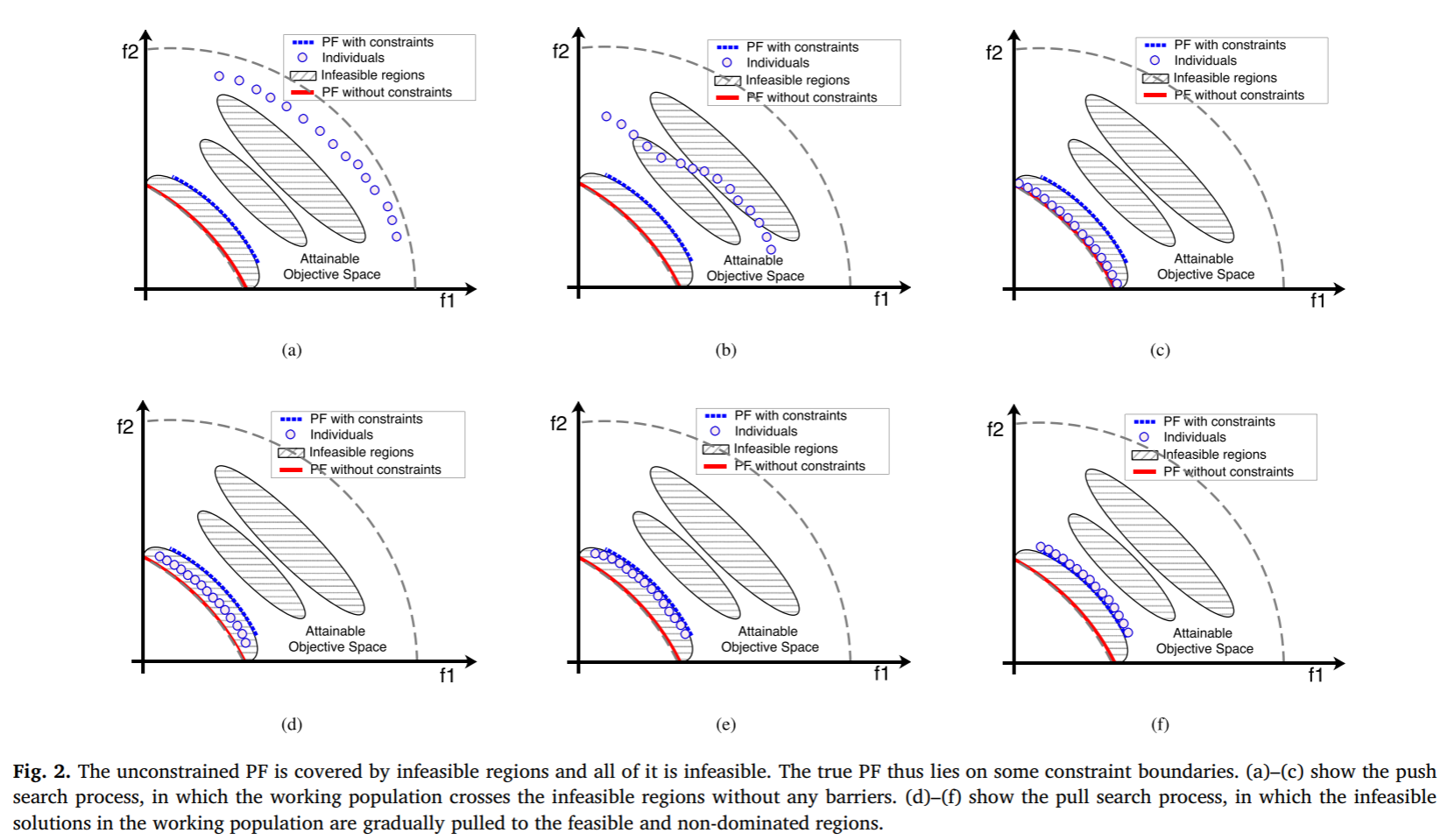
图6 PPS搜索过程示意图
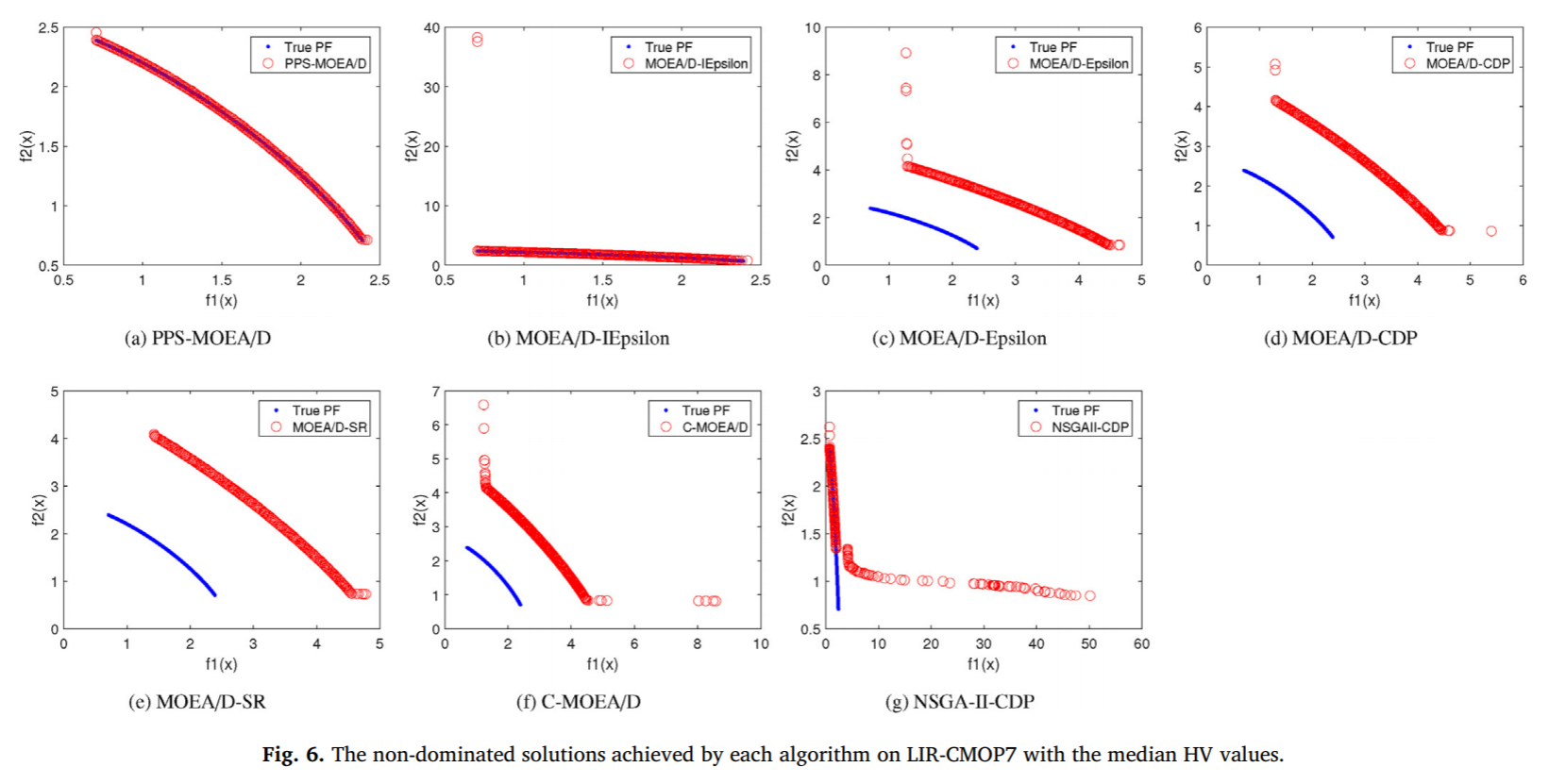
图7 PPS和其他当前最好的6种算法在LIR-CMOP7问题上的对比结果
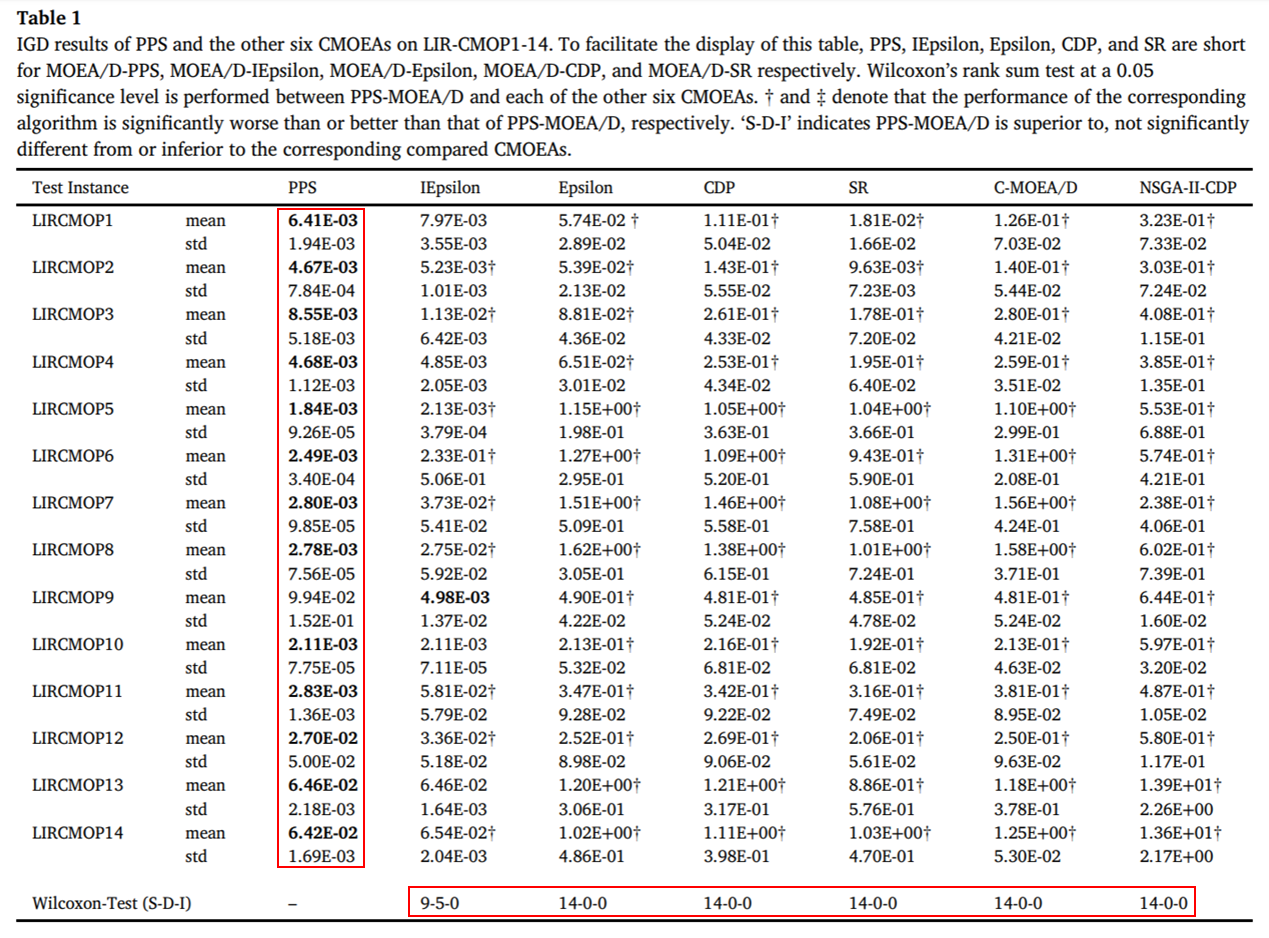
图8 PPS和其他当前最好的6种算法在IGD指标上的对比结果
值得注意的是,PPS是一个非常具有潜力的约束多目标问题求解框架,其中的Push和Pull搜索过程都可以进行自由定制,从而衍生出一系列的约束多目标进化算法。目前,PPS已经成为求解约束多目标优化问题的一个标杆性框架,在连续约束多目标优化领域,几乎所有新提出的约束多目标优化算法不可避免的要在其基础上进行改进或与其进行对比。该项工作目前已经受到加拿大阿尔伯塔大学Witold Pedrycz教授(进化计算领域的权威,SCI一区期刊Information Science杂志主编),Ponnuthurai Nagaratnam Suganthan教授(进化计算领域的权威,SCI一区期刊Swarm and Evolutionary Computation杂志主编)团队的关注和引用。
工业机械臂已经广泛应用在流水线生产车间,但机械臂的示教依然是一项冗长而耗时的工作。特别是一些面向中小批量生产的制造型企业,因加工对象的变化需要对机械臂频繁地重新设计新的操作轨迹,并在控制系统中进行路径编程及示教。而传统的示教方式需要操作人员进行代码编程,或者采集大量的关键点让系统进行路径的自动拟合。两种方式的轨迹示教都是耗时、费力的。
本文《Analysis and Multi-objective Optimization of a Kind of Teaching Manipulator》采用进化设计的方法设计了一款6自由度(DOF)示教机械臂,可对生产线上工业机械臂进行快速轨迹示教(见图9)。生产示教过程中,熟练技工的操作手感直接影响轨迹操作的质量,因此需要对示教机械臂的操作力进行专门的优化设计。把该示教机械臂的设计问题描述成一个约束多目标优化问题:其中为了保证操作者的良好手感,采用了同时最小化操作轨迹最大操作力及操作力的极差作为优化问题的两个目标,同时保证重力敏感的关节在轨迹上保持静平衡。

图9 示教机械臂的工作示意图
通过采用基于PPS(Push and Pull Search)框架的两种约束多目标进化算法PPS-MOEA/D和PPS-M2M对示教机械臂设计优化问题进行求解,获得了比人类工程师设计更优的设计方案(见图10)。同时通过与几种经典的约束多目标进化算法(MOEA/D-ACDP, MOEA/D-CDP, NSGA-II-CDP 以及 CM2M)进行对比,我们发现采用PPS框架,可以有效的提升对应算法在解决机器人实际优化问题的性能(见图11)。

图10 获得的Pareto前沿上的四个端点个体与工程师设计方案对比图
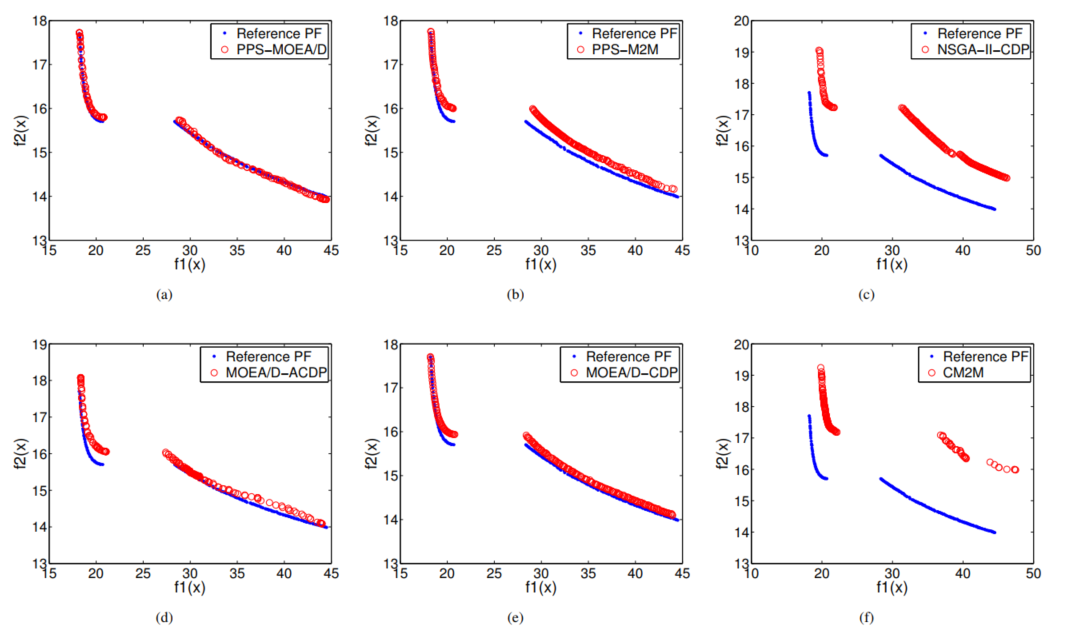
图11 6种算法在示教机械臂设计优化中进行30次独立重复实验中具有最佳HV值的非支配解集
一直以来,约束多目标优化的难点之一是如何在保持多样性和收敛性的同时进行高效的约束处理。由Deb教授提出的约束支配原则(Constraint domination Principle, CDP)已经得到广泛的应用。在CDP原则中,约束违反较小的解总是比约束违反较大的解要好,但这会带来一个问题。如果种群中绝大部分的解是不可行解,那么按照CDP原则,大多数个体的适应值排序将只会按照约束违反的大小来排序,这样在进入下一代的过程中,种群的多样性会急剧下降。
为了克服这一难题,《MOEA/D with angle-based constrained dominance principle for
constrained multi-objective optimization problems》这篇论文提出了一种基于角度约束支配的方法(Angel-based constraint domination principle,ACDP),可概括为三条规则(见图12公式):
(1)当两个比较的解都为可行解时,根据Pareto支配规则判断两解的支配关系。
(2)当两个比较的解至少有一个是不可行解时,如果这两个解在目标空间中的角度小于θ(给定参数),约束违反值小的解支配另一个解。
(3)当两个比较的解至少有一个是不可行解时,如果这两个解在目标空间中的角度大于θ,以概率 pf(其值等于当前种群可行解的比例)视两解为可行解,同时根据规则1判断两解支配关系,以概率 1-pf 视两解互不可比。
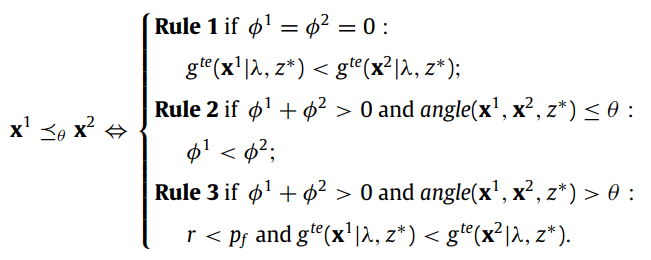
图12 MOEA/D框架下的ACDP定义
所提出的约束处理机制ACDP在MOEA/D框架下进行了实现,在14个基准测试问题和一个工程(和 I 型焊接梁)优化问题上,与6种当前最好的约束多目标进化算法(CMOEAs)对比(见图13)。ACDP算法在IGD指标方面比其他当前最好的算法提升一定数量级(见图14),在保持种群的收敛性、多样性和可行性方面更具优势,充分体现了所提出的约束处理机制ACDP的有效性。
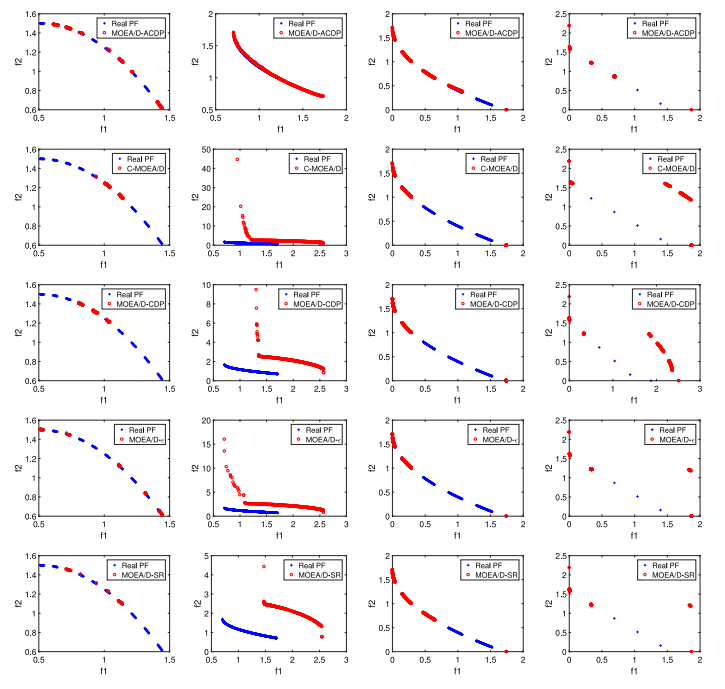

图13 6种不同算法在4个测试问题上得到的非支配解集
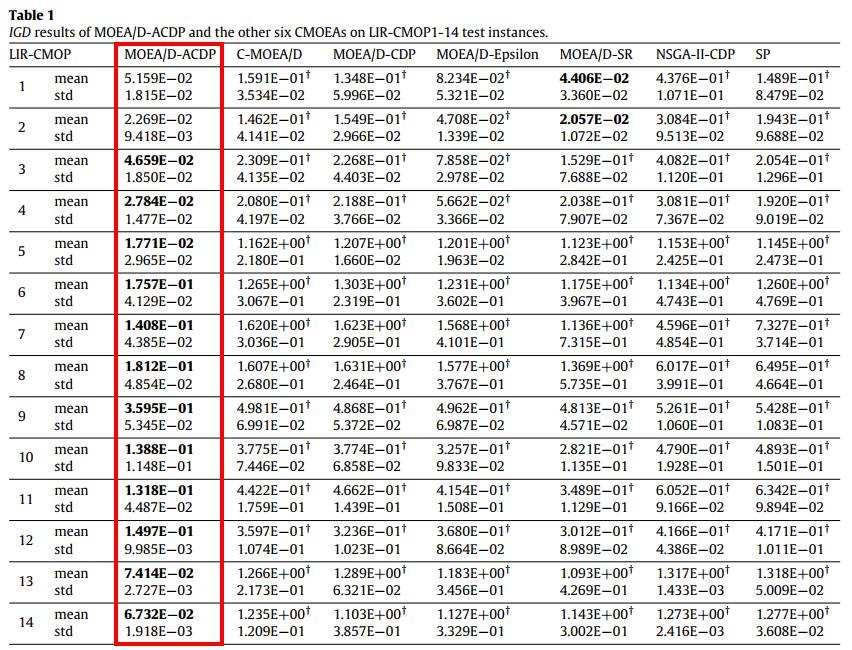
图14 MOEA/D-ACDP和其他6种算法在IGD指标上的对比结果
在《An Improved Epsilon Constraint-handling Method in MOEA/D for CMOPs with Large Infeasible Regions》一文中,针对最初的ε约束方法中ε(k)在进化过程中随着种群代数的增加而逐渐减少,对具有较大不可行区域的约束多目标优化问题并不适用。为了克服这个问题,提出了一种改进的ε约束处理方法(An Improved Epsilon Constraint-handling Method)(见图15公式)。它根据当前总体中可行解的比例动态调整ε(k)的值,以平衡可行区域与不可行区域的探索。与最初提出的ε约束方法相比,它能够在进化过程中增加ε(k)的值,可有效的跨越较大的不可行区域,帮助算法获得收敛性更好的Pareto解集。

图15 改进的ε约束处理方法
所提出的改进的ε约束处理方法嵌入MOEA/D框架下进行了实现,即MOEA/D-IEpsilon。在包括LIRCMOP1-14(不可行区域较大)在内的14个基准测试问题和机器人抓取优化问题上,与MOEA/D-Epsilon, MOEA/D-SR, MOEA/D-CDP和C-MOEA / D四种约束多目标进化算法对比(见图16)。实验结果表明,在所有测试实例上,MOEA/D-IEpsilon明显优于其他4种算法,在IGD指标方面同样优于其他当前最好的4种算法(见图17),充分说明了MOEA/D-IEpsilon适合求解具有较大不可行区域的约束多目标优化问题。
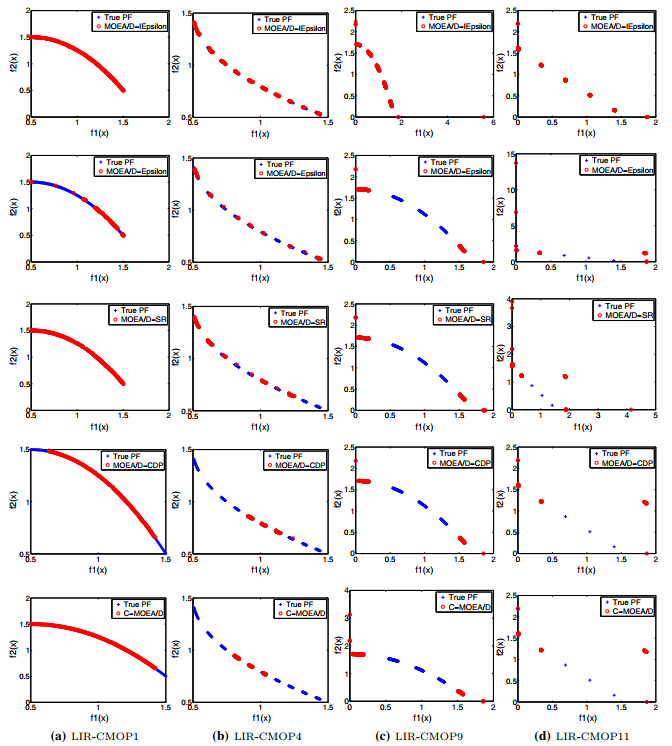
图16 五种不同算法在4个测试问题上得到的非支配解集
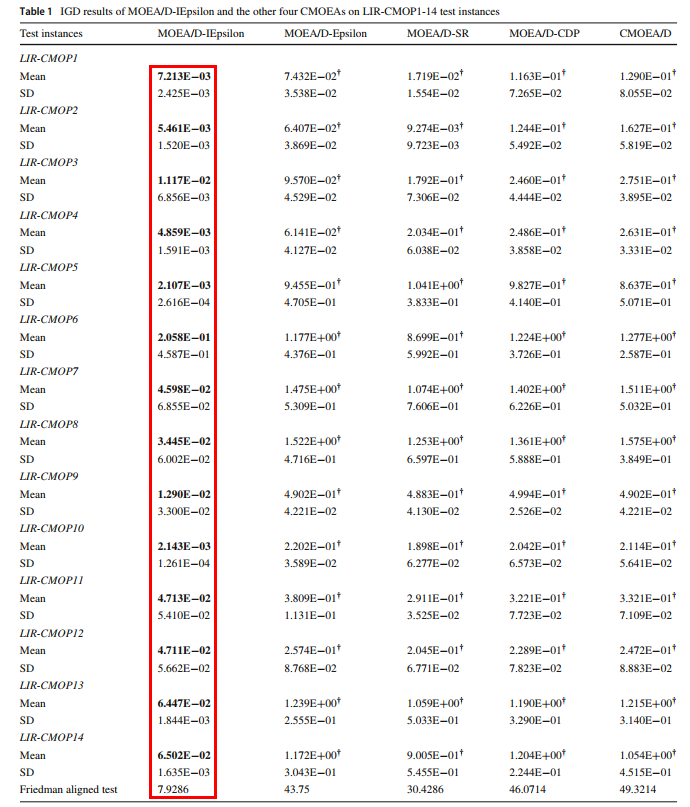
图17 MOEA/D-IEpsilon和其他4种算法在IGD指标上的对比结果
带约束条件的多目标优化进化算法和测试问题集方面的研究是汕头大学人工智能与机器人实验室的一个特色,目前在国际学术界处于领先地位。这些成果可以很好地应用于机器人系统的设计优化,结合实验室开发的《机器人系统设计自动化》软件(已获得软件著作权),在六自由度机械臂及平衡示教机械臂开发方面已经获得了具体的应用,其中平衡示教机械臂已经作为开发的产品销售到企业进行应用。
相关论文信息如下:
-
Zhun Fan, Wenji Li, Xinye Cai*, Hui Li, Caimin Wei, Qingfu Zhang, Kalyanmoy Deb, and Erik Goodman. Difficulty Adjustable and Scalable Constrained Multi-objective Test Problem Toolkit, Evolutionary Computation, DOI: 10.1162/evco_a_00259, 2019. (SCI计算机科学——理论与方法学科1区, IF=2.388) [Download PDF] [CODE]
-
Zhun Fan, Wenji Li, Xinye Cai*, Hui Li, Caimin Wei, Qingfu Zhang, Kalyanmoy Deb, and Erik Goodman. Push and Pull Search for Solving Constrained Multi-objective Optimization Problems, Swarm and Evolutionary Computation, vol. 44, no. 2, pp. 665-679, 2019. ( SCI人工智能1区,IF:3.893 ) [Download PDF] [CODE]
-
Zhun Fan, Yugen You , Xinye Cai*, Haodong Zheng, Guijie Zhu, Wenji Li, Akhil Garg, Kalyanmoy Deb and Erik Goodman. Analysis and multi-objective optimization of a kind of teaching manipulator[J]. Swarm and Evolutionary Computation, 2019, 50: 100554. ( SCI人工智能1区,IF:6.33 ) [Download PDF]
-
Zhun Fan, Yi Fang, Wenji Li ,Xinye Cai*, Caimin Wei, Erik Goodman. MOEA/D with angle-based constrained dominance principle for constrained multi-objective optimization problems[J]. Applied Soft Computing, 2019, 74: 621-633.( SCI人工智能2区,IF:4.873 ) [Download PDF] [CODE]
-
Zhun Fan, Wenji Li, Xinye Cai*, Han Huang, Yi Fang, Yugen You, Jiajie Mo, Caimin Wei, and Erik Goodman, An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions. Soft Computing, 2019: 1-20. ( SCI人工智能2区,IF:2.784 ) [Download PDF] [CODE]
|
